AtCoder Beginner Contest 346

发表于 更新于 分类于 阅读次数： 本文字数： 1.5k 阅读时长 ≈ 6 分钟
Better late than never.

A. Adjacent Product

思路：

  • 按照规则模拟即可

时间复杂度：\(O(N)\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    
    int N;
    std::cin >> N;

    std::vector<int> a(N);
    for (int i = 0; i < N; i++) {
        std::cin >> a[i];
    }

    for (int i = 0; i + 1 < N; i++) {
        std::cout << a[i] * a[i + 1] << " ";
    }
    
    return 0;
}

B. Piano

思路：

  • 注意这个 W 和 B 的范围，最大为 100
  • 那么直接将模板串延长 300 倍，然后枚举求子串是否存在即可

时间复杂度：\(O(N)\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    
    int W, B;
    std::cin >> W >> B;

    std::string S = "";
    std::string p = "wbwbwwbwbwbw";
    for (int i = 0; i < 300; i++) {
        S += p;
    }

    int n = S.size();
    for (int i = 0; i + W + B <= n; i++) {
        std::string s = S.substr(i, W + B);
        int w = std::count(s.begin(), s.end(), 'w');
        int b = std::count(s.begin(), s.end(), 'b');
        if (w == W && b == B) {
            std::cout << "Yes\n";
            return 0;
        }
    }
    std::cout << "No\n";

    return 0;
}

C. \(\Sigma\)

思路：

  • 求 1 到 K 范围内，不在序列 a 中的元素总和
  • 我们直接将求和的技巧转换为，在范围 1 到 K 中，所有元素的总和减去存在于序列 a 的元素和

时间复杂度：\(O(N)\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    
    int N, K;
    std::cin >> N >> K;

    std::vector<int> a(N);
    for (int i = 0; i < N; i++) {
        std::cin >> a[i];
    }
    
    std::unordered_set<int> vis;
    i64 ans = (1LL + K) * K / 2;
    for (int i = 0; i < N; i++) {
        if (vis.count(a[i])) continue ;
        if (a[i] <= K) {
            ans -= a[i];
            vis.insert(a[i]);
        }
    }
    std::cout << ans << "\n";

    return 0;
}

D. Gomamayo Sequence

题目大意：

  • 维护一个字符串，使得在这个字符串里，只存在一个相邻位置是相同的，如 1010101011010101 或者 101011010010101
  • 如果存在多个相同位置，要修改他们使得只存在一个相邻的位置相同，每一个位置的修改需要的花费是 a[i]，要求得到最小的花费去获得一个满足条件的字符串

思路：

  • 要维护出唯一一个相邻两位是相同数的位置，我们可以设如下的状态：
  • 设 f[i][0] 为从前往后当前这一位是 0 ，f[i][1] 为当前这一位是 1
  • 设 g[i][0] 为从后往前当前这一位是 0 ，g[i][1] 为当前这一位是 1
  • 然后，如果上一位是 1，那么我们就需要找到当前这一位是 0 ，这样就不需要修改当前这一位的值，花费为 0。反之，如果当前这一位不为 0，就需要花费 a[i] 的价值转换为 0，所以状态转移方程为：
    • f[i][0] = f[i - 1][1] + (s[i] == '0' ? 0 : a[i])
    • f[i][1] = f[i - 1][0] + (s[i] == '1' ? 0 : a[i])
  • 求 g[i][0/1]只需要倒着来一遍即可

时间复杂度：\(O(N)\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    
    int N;
    std::cin >> N;

    std::string s;
    std::cin >> s;
    s = ' ' + s;

    std::vector<int> a(N + 1);
    for (int i = 0; i < N; i++) {
        std::cin >> a[i + 1];
    }

    std::vector<std::vector<i64>> f(N + 2, std::vector<i64>(2));
    std::vector<std::vector<i64>> g(N + 2, std::vector<i64>(2));
    for (int i = 1; i <= N; i++) {
        f[i][0] = f[i - 1][1] + (s[i] == '0' ? 0 : a[i]);
        f[i][1] = f[i - 1][0] + (s[i] == '1' ? 0 : a[i]);
    }
    i64 ans = 1E18;
    for (int i = N; i >= 2; i--) {
        g[i][0] = g[i + 1][1] + (s[i] == '0' ? 0 : a[i]);
        g[i][1] = g[i + 1][0] + (s[i] == '1' ? 0 : a[i]);
        ans = std::min(ans, f[i - 1][0] + g[i][0]);
        ans = std::min(ans, f[i - 1][1] + g[i][1]);
    }
    std::cout << ans << "\n";

    return 0;
}

E. Paint

思路：

  • 涂色问题，考虑到会覆盖，所以我们只需要倒着枚举涂色情况，这样可以忽略覆盖
  • 然后用 set 维护一下已经被涂色的地方，然后边枚举，边统计即可

时间复杂度：\(O(NlogN)\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    
    int H, W, M;
    std::cin >> H >> W >> M;

    std::vector<std::array<int, 3>> a(M);
    for (int i = 0; i < M; i++) {
        std::cin >> a[i][0] >> a[i][1] >> a[i][2];
    }

    std::unordered_set<int> col, row;
    std::vector<i64> ans(200010);
    for (int i = M - 1; i >= 0; i--) {
        auto [T, A, X] = a[i];

        if (T == 1) {
            if (!row.count(A)) {
                row.insert(A);
                ans[X] += W - col.size();
            }
        } else {
            if (!col.count(A)) {
                col.insert(A);
                ans[X] += H - row.size();
            }
        }
    }
    ans[0] = 1LL * H * W;
    for (int i = 1; i <= 200000; i++) {
        ans[0] -= ans[i];
    }
    int cnt = 0;
    for (int i = 0; i <= 200000; i++) {
        cnt += !!ans[i];
    }
    std::cout << cnt << "\n";
    for (int i = 0; i <= 200000; i++) {
        if (ans[i]) {
            std::cout << i << " " << ans[i] << "\n";
        }
    }

    return 0;
}

G. Alone

题目大意：

  • 给你一个序列 A，我们要求有多少个子区间满足在这个区间里存在一个出现次数为 1 的数
  • 例如 2 2 1 2 1，这个序列，当我们选取 (l, r)，这个区间，我们可以选 (1, 1), (1, 3), (1, 4), (2, 2), (2, 3), (2, 4), (3, 3), (3, 4), (3, 5), (4, 4), (4, 5), (5, 5)这 12 个子区间，在这些区间里，都存在一个数的出现次数为 1

思路：

  • 将每一个区间抽象为一个二维平面上的点，而我们需要求的区间个数，就是这整个二维平面上所有区间的并集大小
  • 针对样例1，将其转换为二维平面的效果如图，整个区间的面积为12，然后我们用扫描线，维护整个二维平面上区间的并集大小
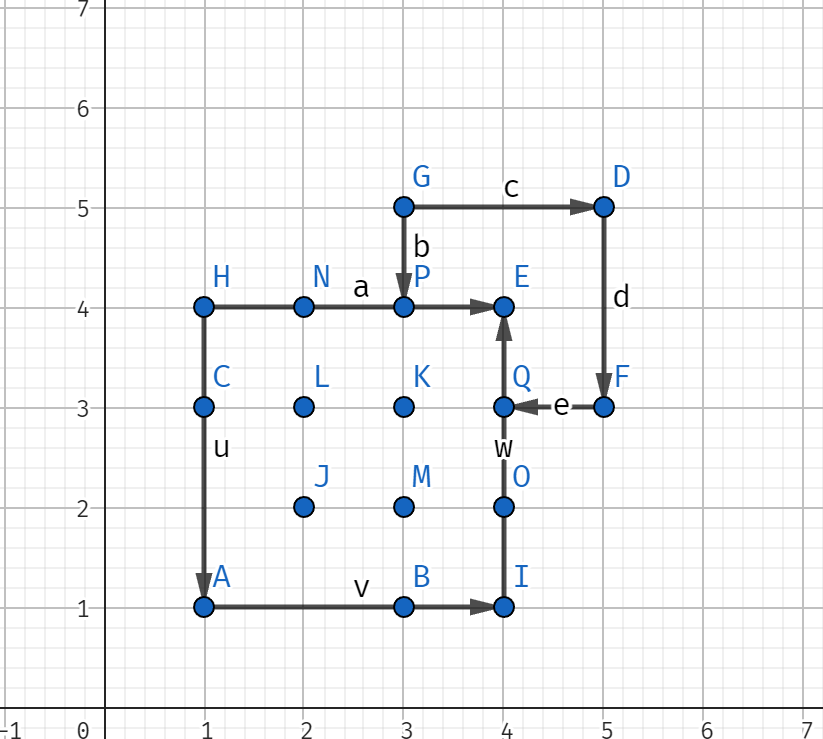
样例1-图解

推荐这个博主讲的题解，很清楚

时间复杂度：\(O(NlogN)\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
constexpr int N = 2E5 + 10;
struct Event {
    int x, y, v;
};
std::vector<Event> e[N];

int val[N << 3], c[N << 3];
void pushup(int u, int l, int r) {
    if (c[u] > 0) {
        val[u] = r - l + 1;
    } else {
        val[u] = l == r ? 0 : val[u << 1] + val[u << 1 | 1];
    }
}
void update(int u, int l, int r, int x, int y, int v) {
    if (x <= l && r <= y) {
        c[u] += v;
        pushup(u, l, r);
        return ;
    }
    int mid = l + r >> 1;
    if (x <= mid) {
        update(u << 1, l, mid, x, y, v);
    } 
    if (y > mid) { 
        update(u << 1 | 1, mid + 1, r, x, y, v);
    }
    pushup(u, l, r);
}

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    
    int N;
    std::cin >> N;

    std::vector<std::vector<int>> b(N + 1);
    for (int i = 1; i <= N; i++) {
        b[i].push_back(0);
    }
    std::vector<int> A(N + 1);
    for (int i = 1; i <= N; i++) {
        std::cin >> A[i];
        b[A[i]].push_back(i);
    }
    for (int i = 1; i <= N; i++) {
        b[i].push_back(N + 1);
    }
    for (int i = 1; i <= N; i++) {
        for (int j = 1; j + 1 < b[i].size(); j++) {
            e[b[i][j - 1] + 1].push_back({b[i][j], b[i][j + 1] - 1, 1});
            e[b[i][j] + 1].push_back({b[i][j], b[i][j + 1] - 1, -1});
        }
    }
    i64 ans = 0;
    for (int i = 1; i <= N; i++) {
        for (auto [x, y, v] : e[i]) {
            update(1, 1, N, x, y, v);   
        }
        ans += val[1];
    }
    std::cout << ans << "\n";
    
    return 0;
}